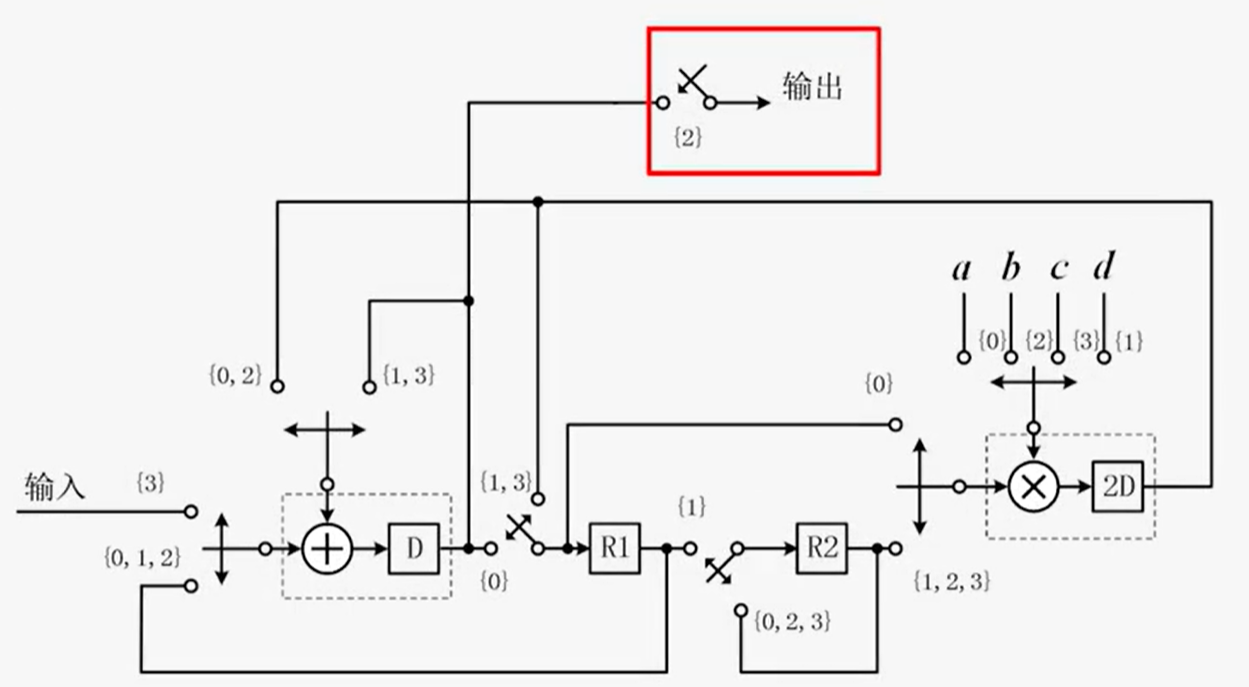
本节主要介绍了VLSI DSP中折叠的基本概念、折叠变换的基本方法（折叠方程）、寄存器最小化技术以及折叠结构的寄存器最小化技术的步骤。
折叠的基本概念
- 折叠：把多个相同运算操作，通过时分复用在单个功能单元上执行，达到资源共享
- 折叠的目的：减小功能单元数目，从而减少面积
- 硬件开销：功能单元减少为$\frac1N$
- 速度代价：处理时间增加为$N$倍
折叠变换
1.定义
考虑节点$U$到$V$延时为$w(e)$的边$U\rightarrow V$，其功能单元分别为$H_u$和$H_v$
折叠因子$N$：折叠到单个功能单元的运算数目
节点$U、V$在硬件中调度执行的时间划分，$0 \sim N-1$
$u、v$是时间分割的顺序标号，节点$U、V$按此顺序被调度执行
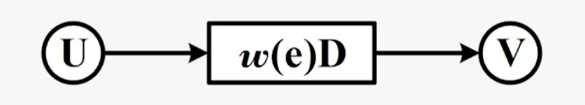
折叠集：执行相同运算功能操作的有序集
- 折叠集中包含N个元素，表示N个运算，其中的一些可能是空运算
- 折叠集中处于第$j(0,1,\cdots,N-1)$个位置的运算，其在第$j$个时间段执行
2.折叠方程
$$
D_F(U\rightarrow V)=Nw(e)-P_u+v-u
$$
- $D_F(U\rightarrow V)$表示有向边$U\rightarrow V$的折叠延时
- $N$为折叠因子
- $w(e)$为$U\rightarrow V$本来的延时数目、
- $p_u$为输入节点的流水线级数
- $v$为输出节点调用时刻
- $u$为输入节点调用时刻
3.画折叠结构
设置折叠集的执行顺序，但前提是需使得折叠系统DFG中所有边都必须满足$D_F(U\rightarrow V)\ge0$
根据折叠方程计算所有路径的折叠延时
根据折叠延时画出折叠结构
以Biquad滤波器为例：以N=4为折叠因子进行折叠
指定两个折叠集：加法折叠集（设置流水线为1），乘法折叠集（设置流水线为2）
- $S1=\{4,2,3,1\}$：加法运算由同一个硬件加法器执行
- $S2=\{5,8,6,7\}$：乘法运算由同一个硬件乘法器执行
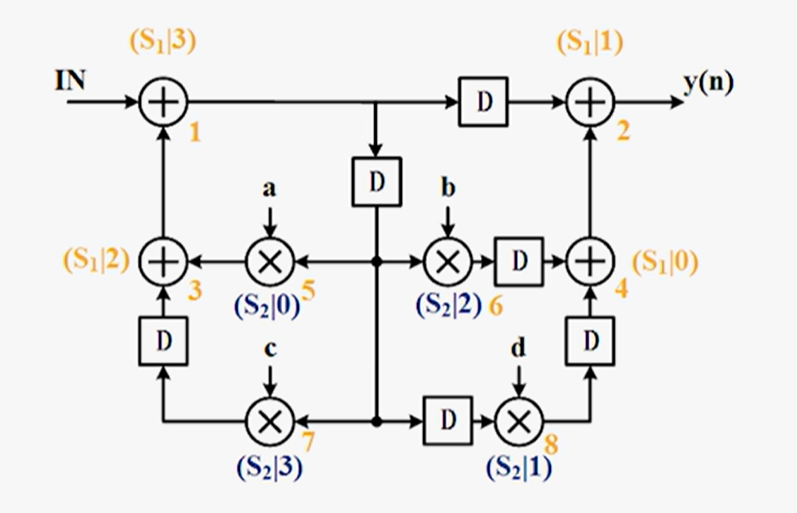
根据折叠方程计算所有边的折叠延时
$$
D_F(1\rightarrow 2)=4\times 1-1+1-3=1
$$$$
D_F(1\rightarrow 5)=4\times 1-1+0-3=0
$$$$
D_F(1\rightarrow 6)=4\times 1-1+2-3=2
$$$$
D_F(1\rightarrow 7)=4\times1 -1+3-3=3
$$$$
D_F(1\rightarrow 8)=4\times 2-1+1-3=5
$$$$
D_F(3\rightarrow 1)=4\times 0-1+3-2=0
$$$$
D_F(4\rightarrow 2)=4\times 0-1+1-0=0
$$$$
D_F(5\rightarrow 3)=4\times 0-2+2-0=0
$$$$
D_F(6\rightarrow 4)=4\times 1-2+0-2=0
$$$$
D_F(7\rightarrow 3)=4\times 1-2+2-3=1
$$$$
D_F(8\rightarrow 4)=4\times 1-2+0-1=1
$$画折叠结构：先画出基本的运算单元，然后一个节点一个节点的看其输入边的折叠延时{}中表示调用时间
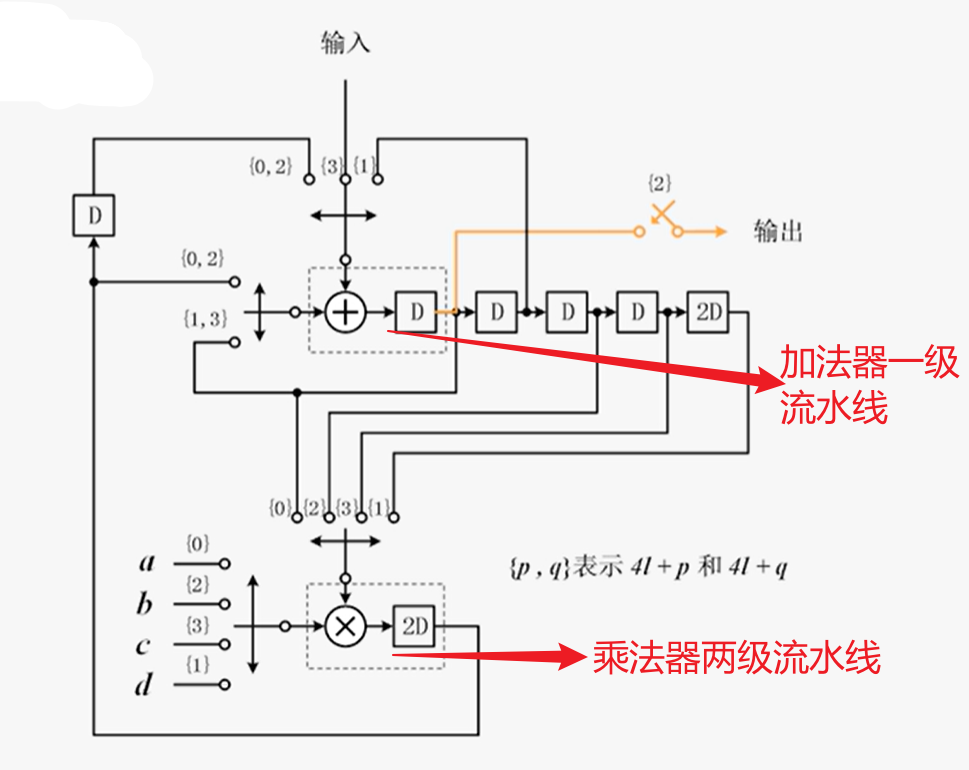
寄存器最小化技术
1.寿命分析
- 定义：折叠会插入寄存器，寿命分析是计算用硬件实现DSP算法所需的最少寄存器数的过程
- 在寿命分析中，算出每个单位时间里的激活变量数，就可以确定任意单位时间里的最大激活变量数，此最大激活变量数则是实现DSP程序所需的最小寄存器数
2.线性寿命图
- 不将变量产生的时钟周期算入激活中
DSP程序通常为周期性的，在考虑迭代时：
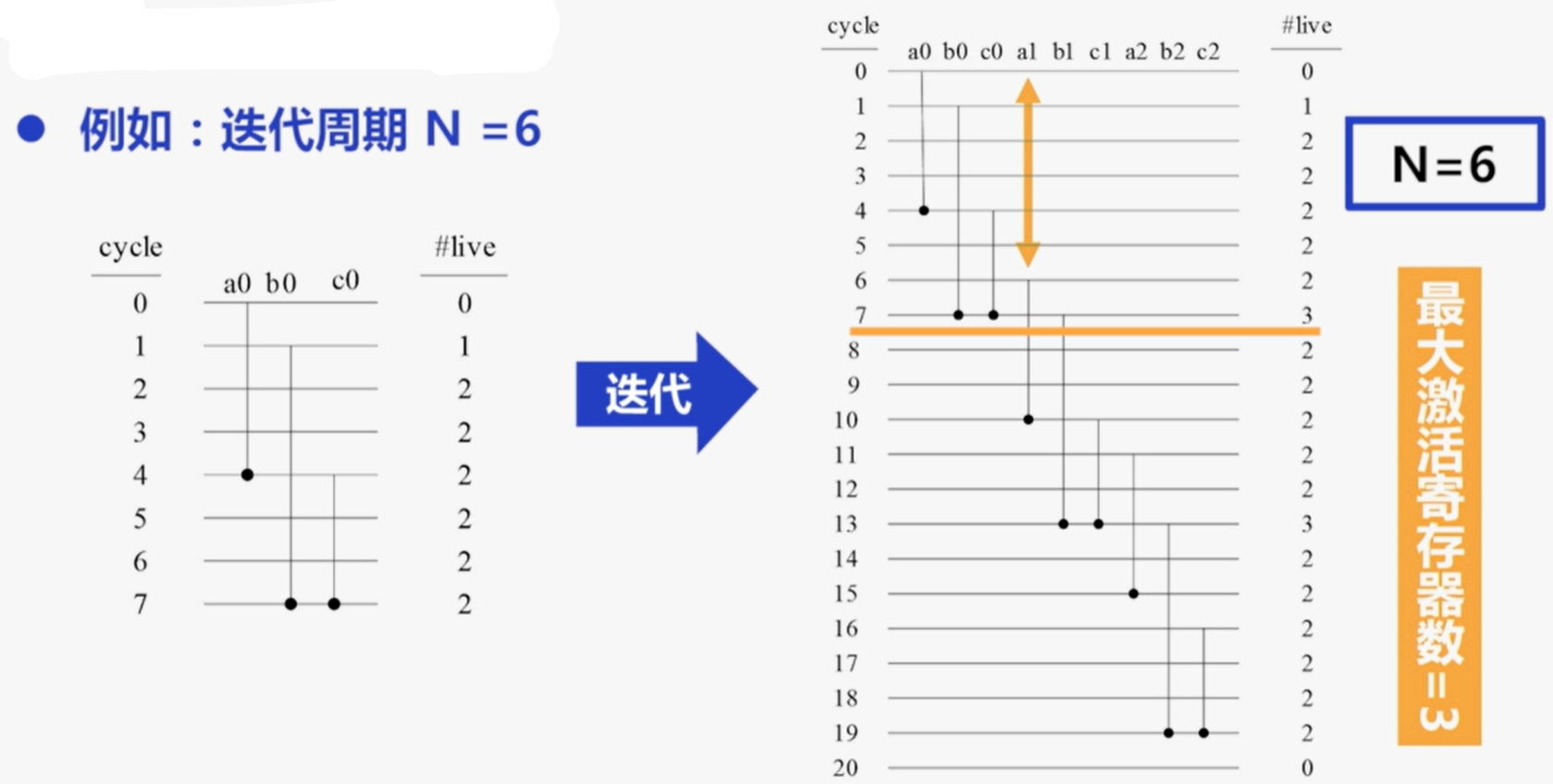
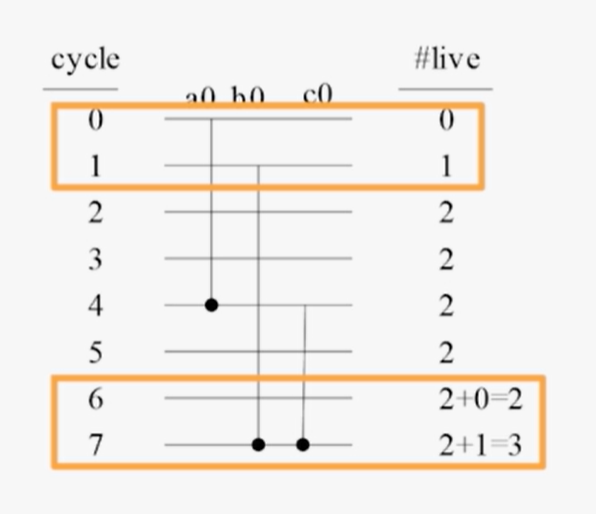
可以仅考虑首次迭代计算出最大激活变量数：
- 因为此时迭代周期N=6，则从第6个时钟周期开始对原有激活数依次加上迭代的激活数直到与上一次数据无重合
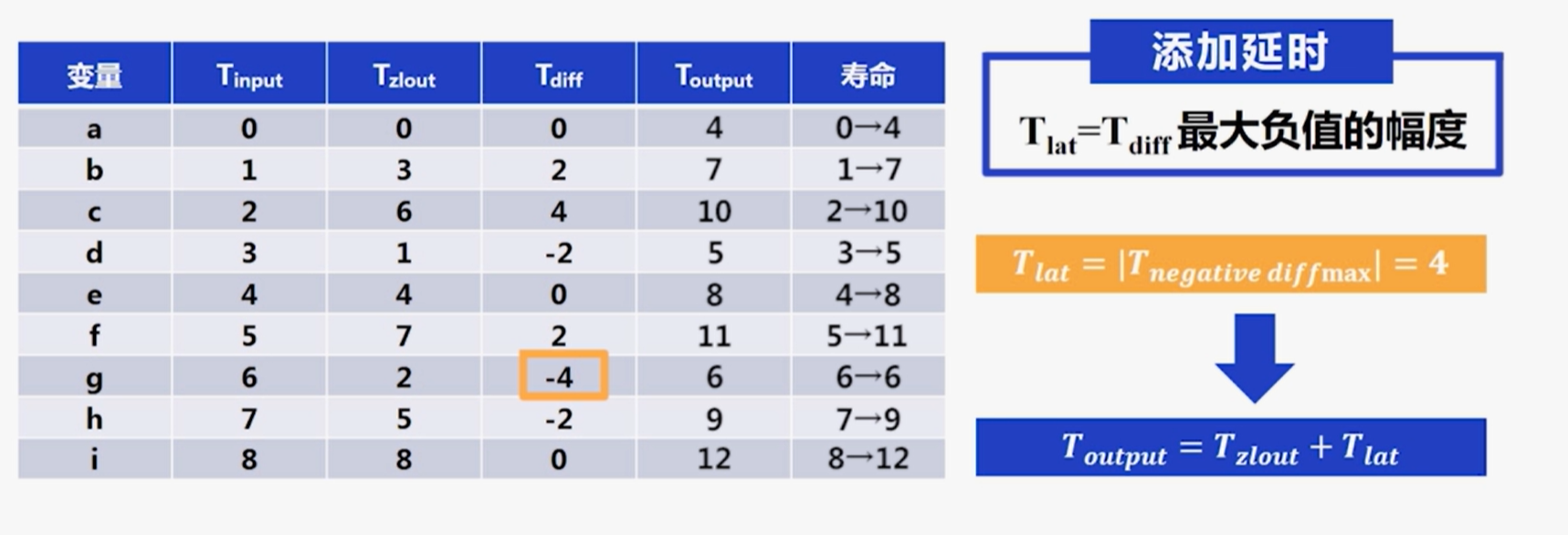
3.寿命表
- $T_{input}$：输入时间
- $T_{zlout}$：0延时输出时间
- $T_{diff}=T_{zlout}-T_{input}$
- $T_{lat}=T_{diff}最大负值的绝对值$
- $T_{output}=T_{zlout}+T_{lat}$：输出时间
- 寿命：$T_{input}\sim T_{output}$
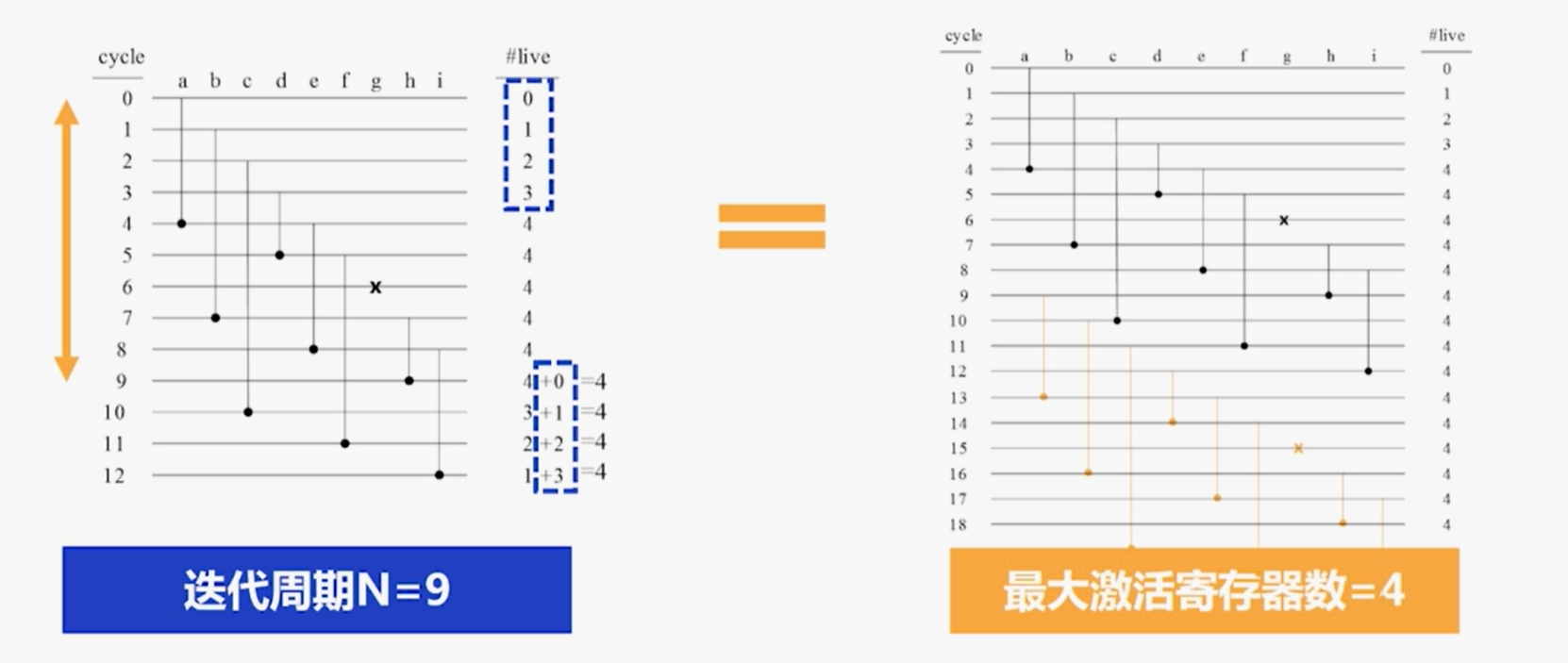
根据寿命表求得的每个变量的寿命，画出线性寿命图从而求出最大激活寄存器数：
4.前向-后向分配技术
- 按逐级前项移位的方式进行数据的传播，直至数据被用到输出端
- $R1、R2、R3、R4$表示四个寄存器
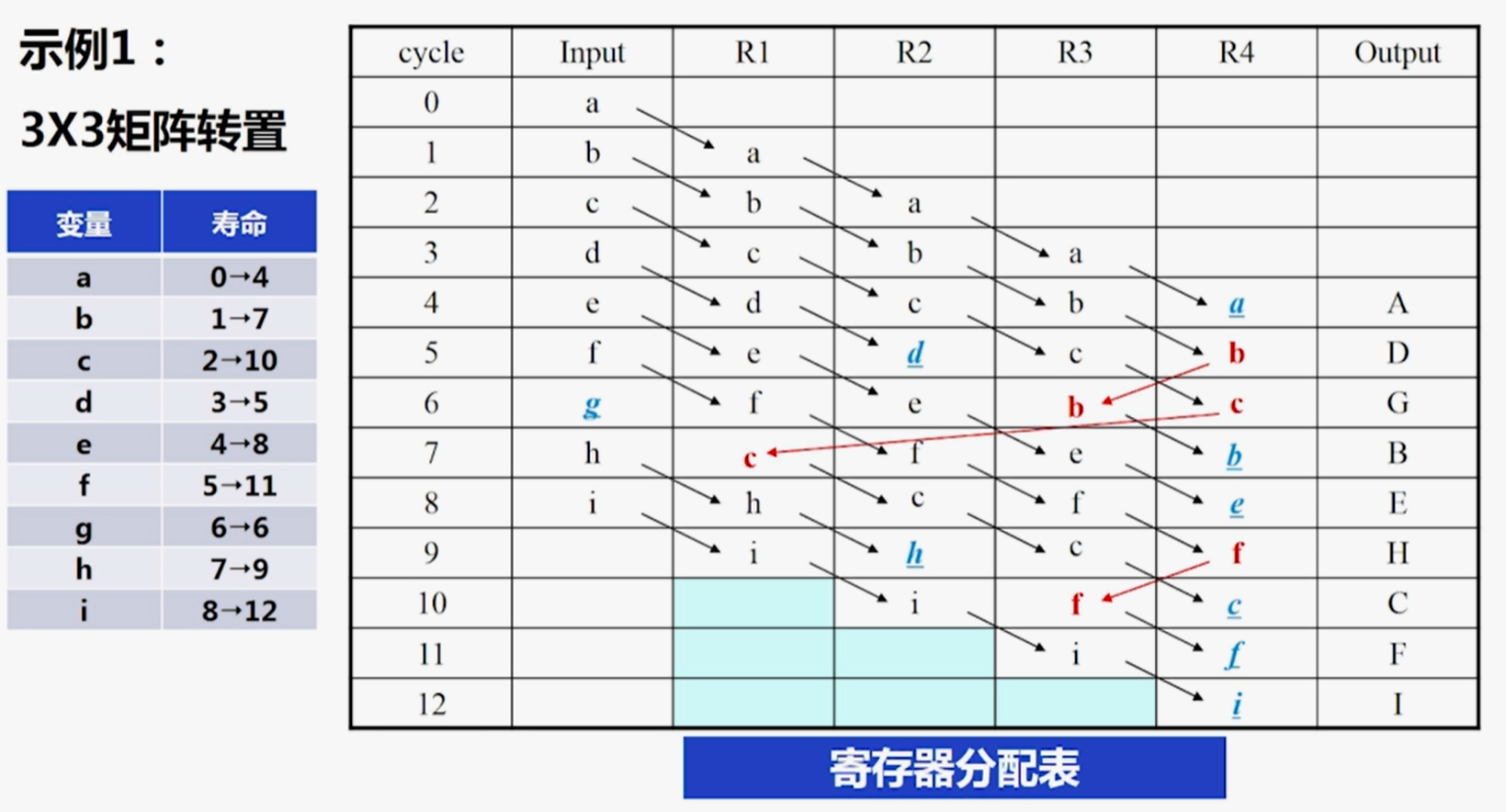
- 通过上述寄存器分配表可以得到折叠后的架构为：
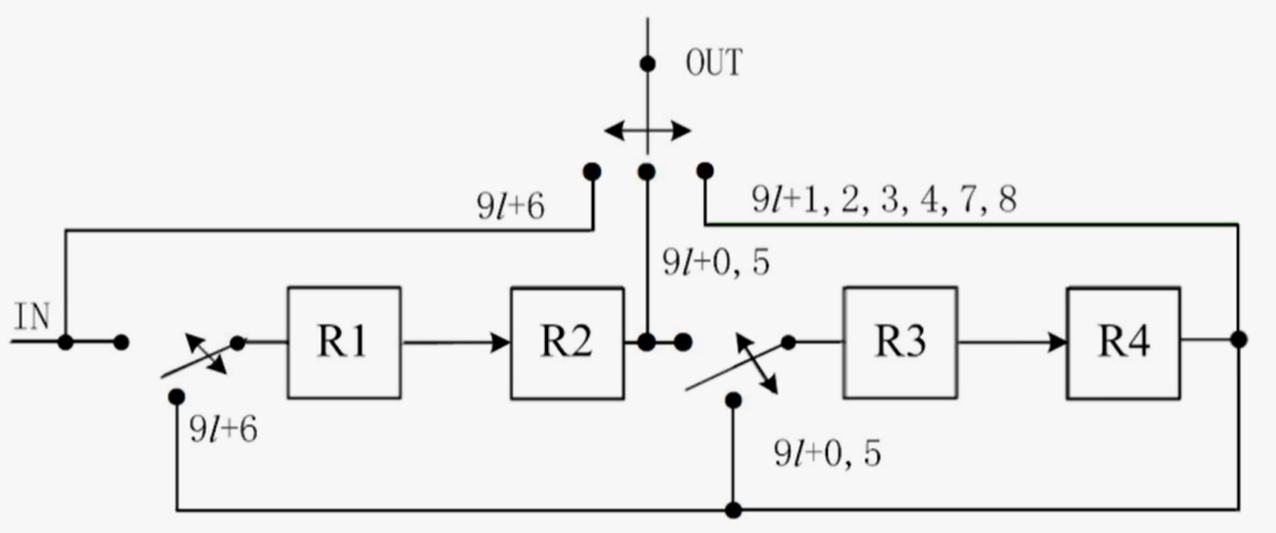
折叠结构的寄存器最小化
- 当折叠延迟存在负数时，按以下六个步骤完成折叠架构的寄存器最小化设计：
- 进行折叠的重定时
- 写出折叠方程
- 用折叠方程构造寿命表
- 画出寿命图并确定所需寄存器数
- 进行前向-后向寄存器分配
- 画出最小寄存器数的折叠架构
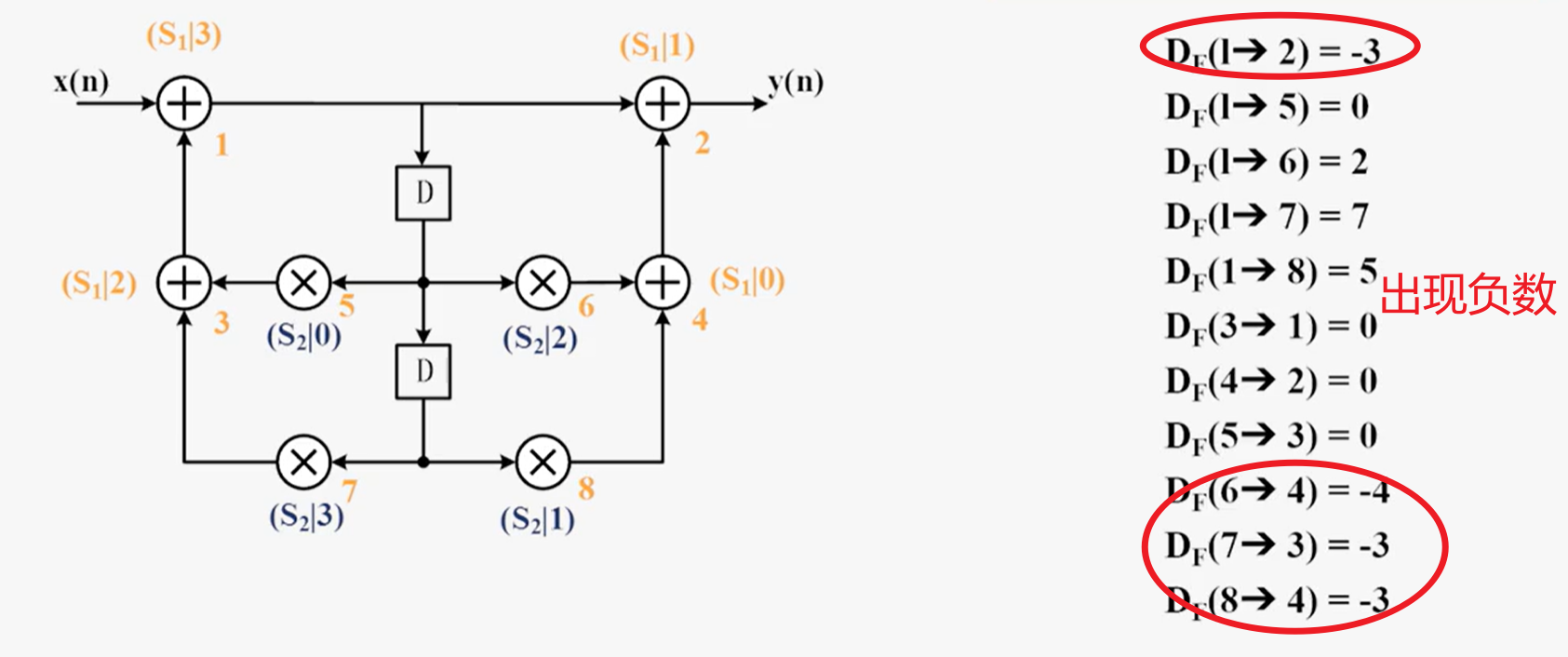
1.进行折叠的重定时
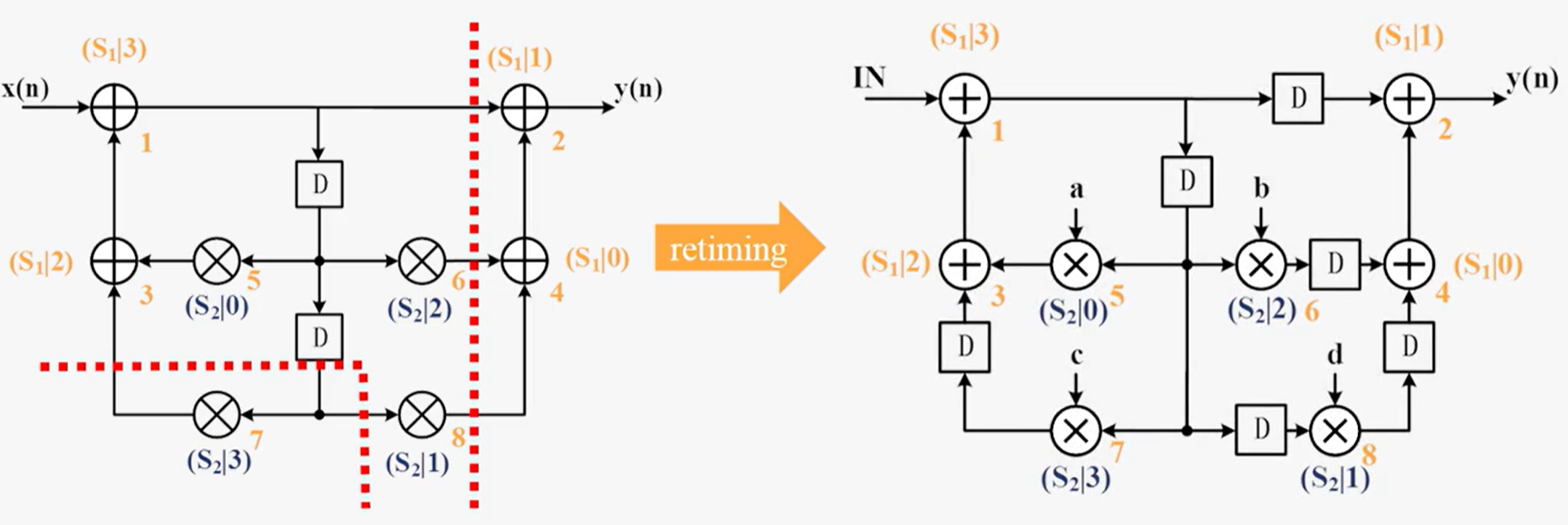
2.写出折叠方程
3.用折叠方程构造寿命表
- $T_{output}=T_{input}+max\{D_F(U\rightarrow V)\}$
- $T_{input}=u+P_u(流水线级数)$
- 寿命：$T_{input}\sim T_{output}$
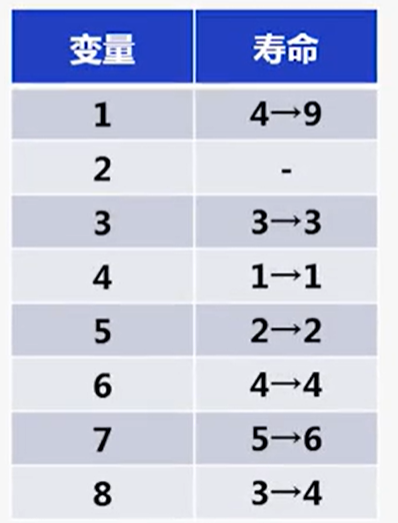
4.画出寿命图并确定所需寄存器数
- 则所需最小寄存器数为2
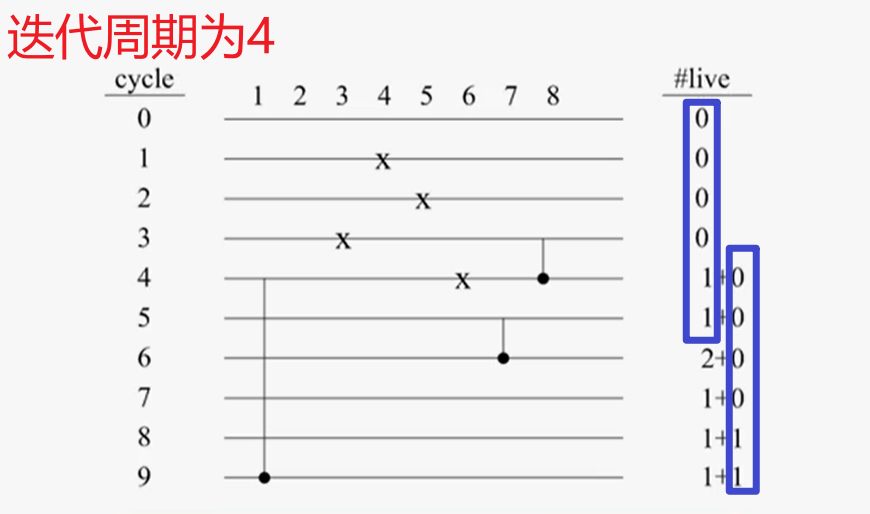
5.进行前向-后向寄存器分配
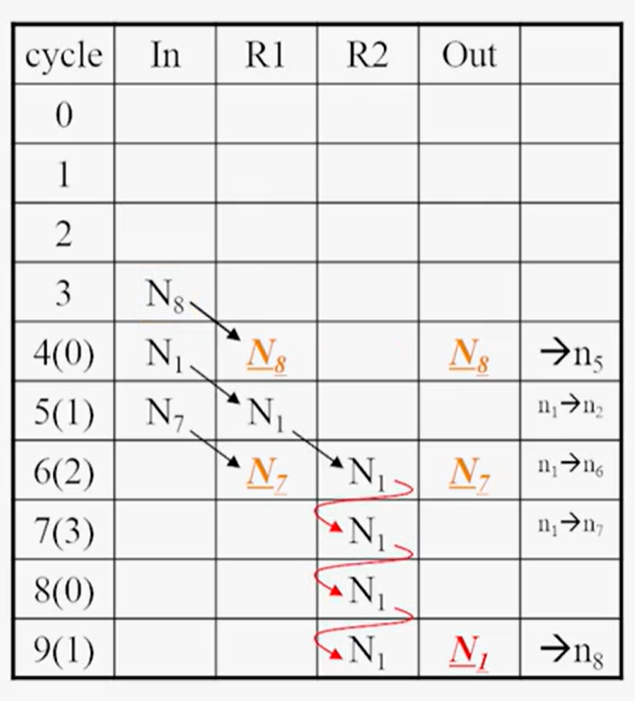
6.画出最小寄存器数的折叠架构
